![]()
I hope you have gone through previous post before reading this post for Learning Rate; because these posts are related and are continuation of the Learning LSTM network.
Difference between Feed Forward Neural Network and RNN.
In the previous post, we have understood how RNN suffers from vanishing gradient. This section of Learning Rate focus on why gradient is so important. Please have a look at the following lines.Gradient means change in error with respect to change in weight. If gradient is steeper it reflects that there is more learning but when gradient is flat it means model stops learning. This was the major draw aback of RNN which was removed by LSTM which we are discussed in this section. This tutorial will cover the following content:
1.) What is LSTM and how it eliminate the problem of vanishing gradient.
2.) Understanding LSTM in deeper sense with all gates
What is LSTM and how it eliminate the problem of vanishing gradient?
Solution to vanishing gradient was provided by German researcher’s Sepp Hochreiter and Juergen Schmidhuber in mid of 1990 in introducing LSTM. LSTM stands for Long Short Term Memory. They are special kind of RNN which have the capabilities of learning long term dependencies. From long term dependencies I mean that they understand the context using the knowledge of previous word and need not to start from scratch every time. We will go to details of the LSTM afterwards. Firstly let us provide the simple solution to the question how LSTM solved the problem of vanishing gradient. If you keep your memory back and think how the gradient is back-propagated in RNN, you will notice that while calculating the gradient in the previous states it degrades as activation functions or of activation function is never unity and gradient is calculated as the product of activation function or derivatives of activation function. This case is not true for LSTM which have the activation function or derivative of activation function equals to unity which does not vanish the gradient while propagating backwards. This is just the simple definition and we will go into the deeper sense as we will move on so there is nothing to worry if you have not understood above.
Understanding LSTM in a deeper sense
Key part of LSTM is the cell state. Information can be stored in it and can be taken from it. Cell makes the decision what to store and what not to through gated mechanism. We will discuss about these gates in the following subtopics. These gates are analog and are implemented using the activation functions. Just think about the NAND, AND OR gates which you have studied. They are also made with the combination of each other. Advantage of being these gates being analog is that analog function is differentiable, hence much suitable for the back propagation. Since these gates are made from the activation function hence they carries some weight. These weights are updated during the back propagation. Gates compare the weight of input signal with the threshold it sets and hence it forms a filter. Some input is allowed and some not. In this way system learns. Before moving ahead it is important to discuss about these gates. Please see the below image before studying gates.
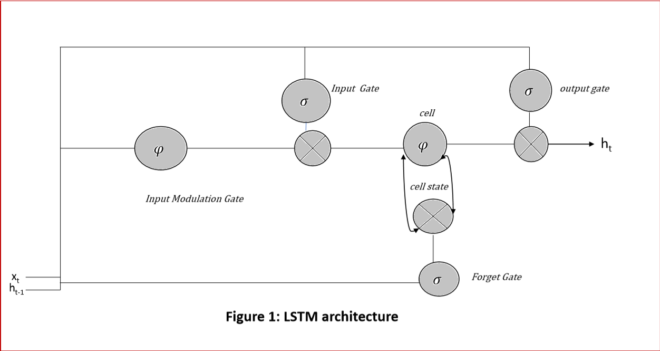
- Forget Gate It is also called as remember vector. It is first of four gates. Please refer to the Figure 1: Detailed Structure of a LSTM Cell. A is the neural network in the figure where Xt is the current input and ht-1 is the previous state. Mathematically it is calculated as below
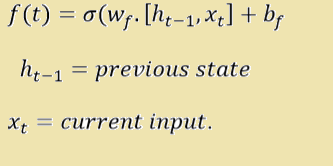
Equation resembles with the equation of the straight line
What is the importance of forget gate
If you want to forget the previous context, forget gate f(t) will be zero. This gate will decide whether complete information is needed or information needs to be forget, To speak in broader sense, it calculates how much of current data should be remembered. A forget gate is responsible for removing the information from the cell state. Let us take an example to understand it in more deeper sense
“Ram is hardworking. Sahil is his friend”
When such word is fed to LSTM machine. When the first full stop is encountered, machine thinks that there may be change in the context so it forgets the subject and this space is kept vacant for the next subject. So subject Ram is replaced by Sahil. This process is achieved with the help of forget gate.
- Input Gate: It is also called as save vector. This is another activation function σ whose value lies between 0 and 1. It is one of the input to the cell like forget gate, It determines which of the input to be passed to the output gate and which to ignore. Please refer to the figure 1 for looking for the input gate. Let us drive the equation for the input gate as below:
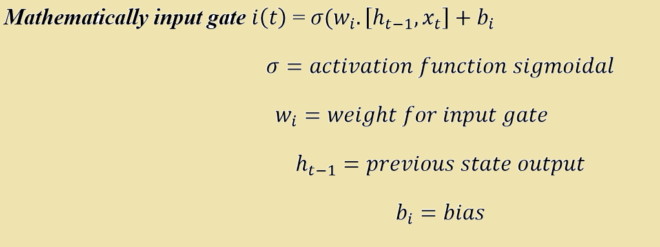
- Input Modulation Gate: Before discussing this further there may a question in minds of the readers that why there is input modulation gate when we have input gate. Question is quite logical and solution to above is as below. Let us revise the equation of cell. If you look at the Figure 1 carefully you will come to know that cell has component called constant error carousel (CEC). Core of cell has a self-connected recurrently linear unit which is also called the memory of LSTM cell. If you look more precisely one can tell that cell gets input from three gates. One is forget gate, other is input gate and last is input modulation gate. Again question why there is need of input modulation gate when we have input gate as well as forget gate. Please see the below image which will make the things more clear.
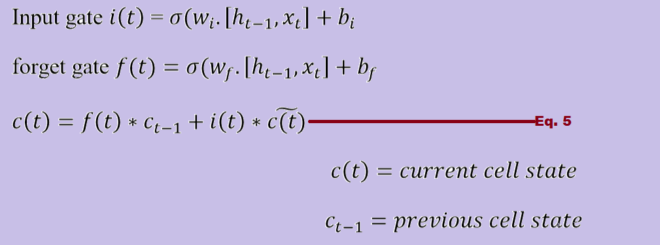
We need such equation which have the value either 0 or 1 because it will help us to forget the information completely or store the information. If you look at the range of σ = [0 1]. If we do not include φ whose range is [-1 1]. Equation 5 will never become zero. Hence information will never be forgotten.
- Output Gate: It is also called as focus vector. This gate decides which information is to be passed at output or which not. Please refer to the figure 1. Let us represent it mathematically
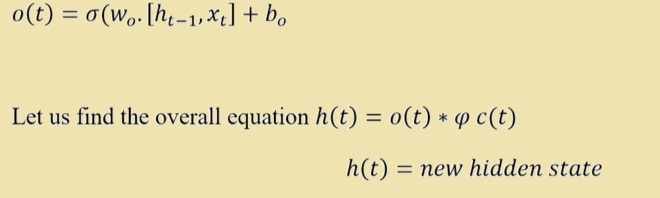
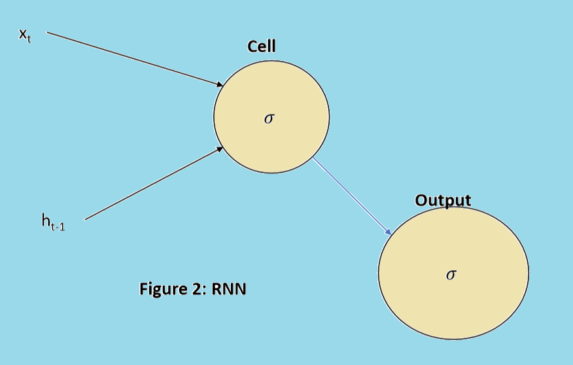
Note: Please look at the figure 1 and figure 2 precisely. Figure 1 represents LSTM architecture whereas Figure 2 represents RNN architecture. RNN does not contain gates to control information to be stored by cell or memory. So gated network of LSTM makes it different from RNN architecture.
Also Read:




I have really loved the way you guys write the blog and especially this one.
I found all the images very useful and easy to understand the topic
Thanks for such message.